行列（Matrix）

はっきりと言いますと、3Dにはそれなりの知識が必要になります。行列や三角関数はもちろん、3Dの用語や手法についての知識が欲しいです。ですが、ここではあまりそのようなことに触れずにいこうと思います。私も深く理解しているわけではありませんから。

と、言い切るのは簡単ですが、全く知らないで3Dを扱うこともまた色々と問題です。すこしは知らなければなりません。そういうわけで今回は「利用することだけに的を絞った行列」です。

頂点

３次元空間の中での頂点は「X,Y,Z」の三つの座標を持っています。この三つの座標があれば、３次元世界の任意の一点を示すことが出来ます。

頂点の移動

たとえば、ある１つの点が与えられたときにその点をx軸を軸にして回転させるにはどうしたらいいでしょうか？難しいですね。ですが、DirectXにはこういう難しい演算を行ってくれる構造体があります。それがMatrixです。

Matrixの中に入っているのは変形の手順

大事なのは「Matrix」の中に入っているのは頂点を移動させる手順だと言うことです。つまり、関数と同じです。

「ある頂点とMatrixを掛け算することによってその頂点を移動させる」こういう事をするためにあるのです。

点を移動させるということ、立体を変形させるということ

ここにあるMatrixがあります。それを立体を作るための頂点配列全部に使ったらどうなるでしょうか？

１つ１つの点は移動しますね。そして移動したあとの点を使って立体を表示させると・・・どうなるでしょうか？

立体が変形することになりますね。

ここで言いたいことはMatrixは３次元世界の中にある全てのものを変形させる事が出来るということです

カメラ、ワールド変換とは？

結局の所「カメラ」「ワールド変換」でそれぞれ行われているのは頂点を行列によって移動・回転・拡大縮小させることなのです。もっと詳しく知りたい方は、本を読んで勉強するのが良いでしょう。

変形を組み合わせる

前回でしたこと、今回覚えたことを合わせて、ちょっと次のことをしてみましょう。

全軸に２倍に拡大、X軸に３０度回転、Y軸に＋１。

上の動作は行列の掛け算で実現できます。

device_.Transform.World =
    Matrix.Scaling(2,2,2)
    *Matrix.RotationX((float)(60f * Math.PI / 180f))
    *Matrix.Translation(0,-2,0);

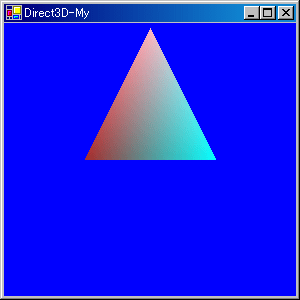
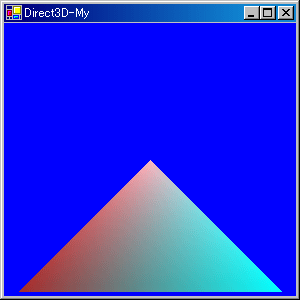
ここで行列の大事な性質を話しておきます。行列では掛け算の順番によって結果が変わります。これはとても大切なことです。数式を出して説明しても良いのですが、めんどくさいのでパスです。

device_.Transform.World =
    Matrix.Scaling(2,2,2)
    *Matrix.Translation(0,-2,0)
    *Matrix.RotationX((float)(60f * Math.PI / 180f));

そのため、大抵は「拡大縮小*回転*移動」の順番で掛け算を行います。

次回は立方体を作りましょう。その次は多分インデックスバッファです。